Simple Harmonic Motion
Guiding Questions
- What are the characteristics of periodic motion? How can we study and
describe such motion?
- How can circular motion be related to simple harmonic motion (SHM)?
- How do we analyse simple harmonic motion?
Learning Outcomes (LOs)
- describe simple examples of free
oscillations.
- investigate the motion of an
oscillator using experimental and graphical methods.
- understand and use the terms
amplitude, period, frequency and angular frequency.
- recognise and use the equation a
= - ω2 x as the defining equation of simple harmonic motion.
- recall and use x= x0
ω sin( ωt )as a solution to the equation a = - ω2 x
- recognise and use v = v0
cos ( ω t ) ,
- describe with graphical
illustrations, the changes in displacement, velocity and acceleration
during simple harmonic motion.
- describe the interchange between
kinetic and potential energy during simple harmonic motion.
- describe practical examples of
damped oscillations with particular reference to the effects of the
degree of damping and the importance of critical damping in cases such
as a car suspension system.
- describe practical examples of
forced oscillations and resonance.
- describe graphically how the
amplitude of a forced oscillation changes with driving frequency near to
the natural frequency of the system, and understand qualitatively the
factors which determine the frequency response and sharpness of the
resonance
- show an appreciation that there
are some circumstances in which resonance is useful and other
circumstances in which resonance should be avoided.
Learning Experiences
- Examine representations used in oscillations
- Examine how different graphs are used to represent SHM. Draw links
between the different graphs highlighting the positive and negative
values and their interpretation. These will help students to
understand SHM as a function of two variables (space and time) and
understand the treatment of vector and scalar quantities .
- Investigate factors affecting period of oscillations using experiments
or a simulation
- Design and carry out an
experiment to build a pendulum or spring-mass system to
obtain a prescribed period. Present the experimental design,
explaining the factors that determine the period of the oscillating
system. This provides an opportunity for students to predict and
collect data to ascertain the properties of a system and determine
whether a motion is considered to be SHM. Students are also to
understand that it is necessary for oscillations to be small for the
motion to be considered as SHM. Students can also be shown other
systems that demonstrate SHM
. Simulations [1]
[2]
[3]
, can also be used for students to investigate these factors.
- Investigate phase using a turntable or a simulation
- Investigate phase using a turntable
or a simulation
to associate each position in an SHM with a position on a uniform
circular motion. This idea can be extended to the phase difference
between different positions in an SHM. The association of SHM with
uniform circular motion helps students to visualise many aspects of
SHM. Students are to make mental links between three related ideas:
physical position and velocity of the oscillator, angle in the
associated uniform circular motion and the position of the
oscillator on a displacement-time graph .
- Build a model for SHM using a datalogger or simulation
- Investigate the motion of a SHM system (pendulum, mass-spring
system) using a datalogger
or a simulation
. Students are to practice observing the motion and interpreting
graphs before getting into the mathematical details of the
equations. Compare the relationship between the different variables
particularly note the values of these valuables at equilibrium
position and at endpoints. Students should practice converting one
graph into another.
- Explore modelling of oscillation in molecules as SHM
- Explore how oscillations of molecules bounded by the van der Waals
interaction can be SHM if the amplitude is small [4]
.
- Explore benefits and danger of resonance
10. Simple examples of free oscillations LO(a)
10.1 YouTube of many examples of oscillators
http://youtu.be/VKtEzKcg6_s
This video can be used at the start of the first lecture (while students
settle down for lecture) to introduce oscillations, to show various modes
of oscillations and to interest them.
10.1.1 Example 1: Simple pendulum
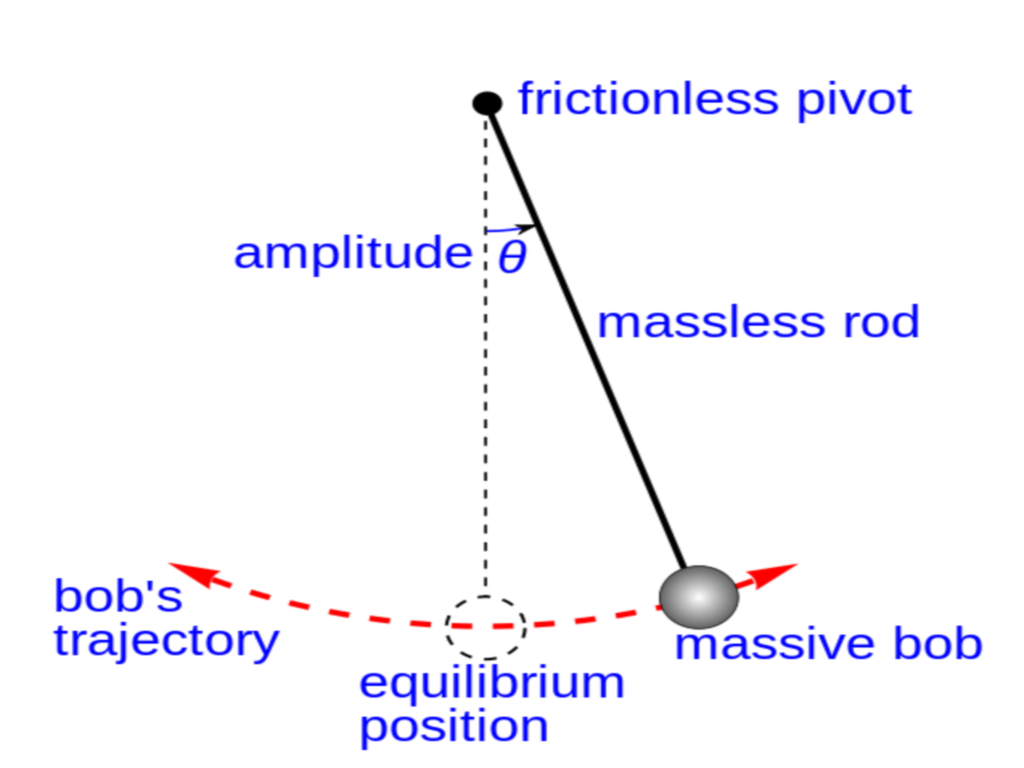
Static picture of a pendulum bob given an initial horizontal displacement
and released to swing freely to produce to and fro motion
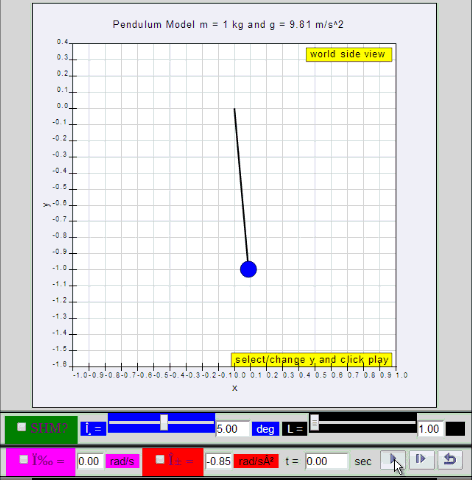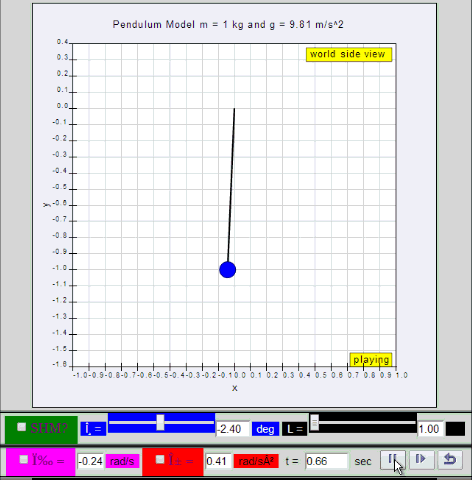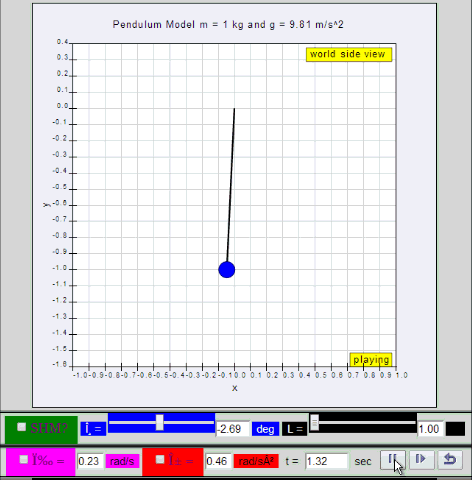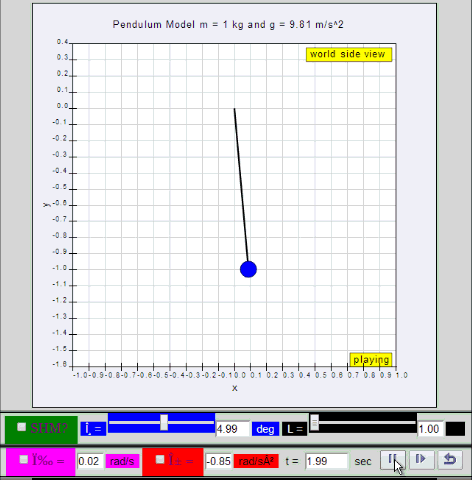
Dynamic picture of a pendulum bob given an initial horizontal displacement
and released to swing freely to produce to and fro motion
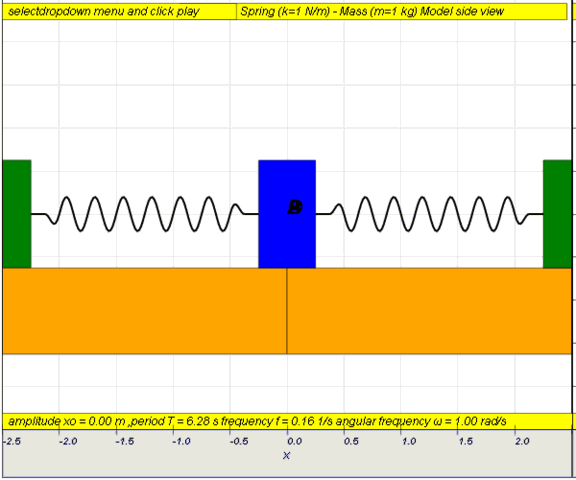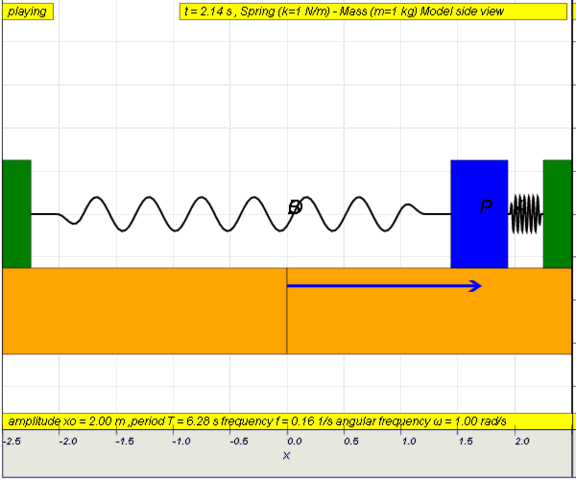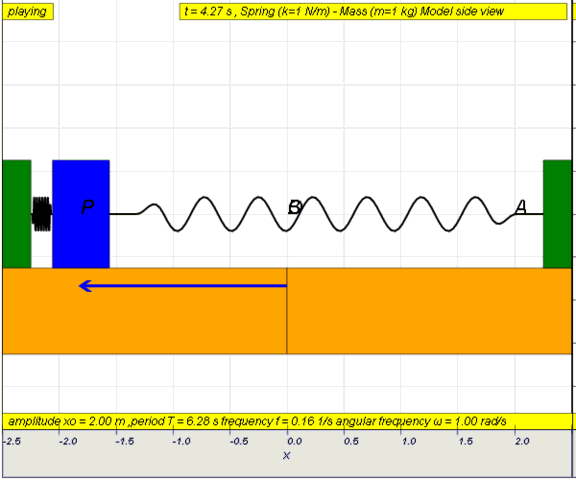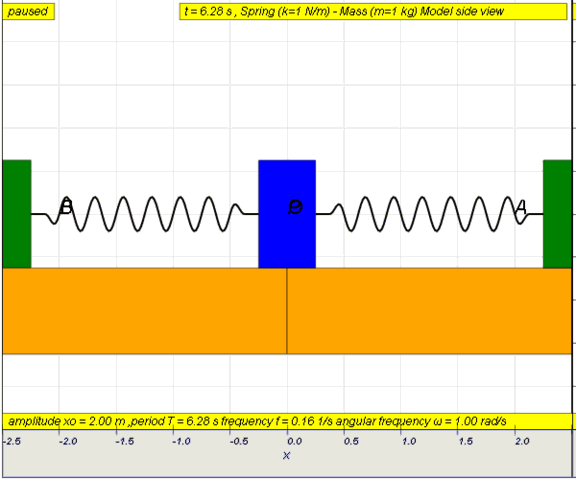
10.1.2 Run Model:
- Run
Sim
- http://iwant2study.org/ospsg/index.php/67-shm01
10.1.2.Q1: what is the maximum angle of release before the motion is not
accurately described as a simple harmonic motion for the case of a simple
free pendulum?
10.1.2.A1: : 10 degrees for error of , depending on what is the error
acceptable, small angle is typically about less than 10 degree of swing from
the vertical.


